Proporção Áurea: o número de ouro

A razão ou proporção áurea representa a mais agradável proporção entre dois segmentos ou duas medidas, é uma procura constante da harmonia e da beleza que leva Piet Mondrian a encontrar a matemática.

Mondrian descobriu o famoso número de ouro e com ele chegou ao retângulo de ouro. Partilhou com Da Vinci a ideia de que a arte deveria ser sinônimo de beleza e movimento contínuo, por isso ambos utilizaram o retângulo de ouro.

A razão de ouro exprime movimento, pois mantém-se em espiral até ao infinito, e o retângulo de ouro exprime a beleza, pois é uma forma geométrica agradável à vista. Assim, o retângulo de ouro passou a ser presença constante em suas pinturas.

Perfeição e harmonia

O número de ouro é um valor numérico aproximado de 1,618. Este número irracional é considerado por muitos o símbolo da harmonia.

O número de ouro é exatamente (1+raiz quadrada(5))/2, que aproximadamente é 1,618033988749894848204…

O número de ouro é considerado como sendo a “proporção divina” e foi utilizado ao longo da história, em variados contextos:

• Na Grande Pirâmide de Gizé, construída pelos egípcios, o quociente entre a altura de uma face pela metade do lado da base é quase 1,618;
• A Fídias atribui-se a construção do Partenon Grego em Atenas, templo representativo do século de Péricles, usando o Retângulo de Ouro (a razão entre o comprimento e a largura é o número de ouro) na sua base e fachada;
• Euclides, no seu livro “Os Elementos”, utilizou o número de ouro para construir o primeiro pentágono regular e os dois sólidos regulares mais complexos, o dodecaedro (12 faces pentagonais) e o icosaedro (20 faces triangulares);
• Os Pitagóricos usaram também a seção de ouro na construção da estrela pentagonal;
• A contribuição de Fibonacci ou Leonardo de Pisa para o número de ouro está relacionada com a solução do problema dos coelhos publicado no seu livro Liber Abaci, que deu origem à sequência de números de Fibonacci: as sucessivas razões entre um número e o que o antecede vão-se aproximando do número de ouro;
• Frei Luca Pacioli publicou em 1509 um livro com o titulo de “De Divina Proportione”, com ilustrações de sólidos platônicos realizados pelo seu amigo Leonardo Da Vinci, no qual relaciona o número de ouro polígonos regulares e sólidos platônicos;

• 

  Kepler baseou a sua teoria cósmica nos cinco sólidos platônicos e na sua relação com o número de ouro;

• Le Corbusier (arquiteto francês) e Salvador Dali são dois dos muitos artistas que utilizam o número de ouro nas suas obras.

O número é também utilizado para desenhar espirais semelhantes às que encontramos na Natureza, por exemplo, no centro dos girassóis, nas pinhas e nos moluscos

Na atualidade algumas construções, como por exemplo, o edifício das Nações Unidas, em Nova Iorque, e até objetos do dia a dia, como, por exemplo, o cartão de crédito, estão ligados ao retângulo de ouro e desta forma estão ligados ao número de ouro.

Retângulo de ouro

Se desenharmos um retângulo cuja razão entre os comprimentos dos lados maior e menor é igual ao número de ouro obtemos um retângulo de ouro.

O retângulo de ouro é um objeto matemático que marca forte presença no domínio das artes, nomeadamente na arquitetura, na pintura, e até na publicidade. Este fato não é uma simples coincidência já que muitos testes psicológicos demonstraram que o retângulo de ouro é de todos os retângulos o mais agradável à vista.

Construção de um retângulo de ouro

Basta seguir as indicações e ter à mão uma folha de papel, um lápis, compasso e uma régua ou esquadro.

1. Desenhar um quadrado qualquer na folha (o lado do quadrado será a largura do retângulo de ouro);
2. Marcar os pontos médios dos lados de “cima” e de “baixo” do quadrado;
3. Traçar a reta que passa pelos pontos médios (verificar que o quadrado ficou dividido em dois retângulos congruentes);
4. Num dos retângulos traçar uma das suas diagonais.
5. Com o compasso desenhar a circunferência que tem centro no ponto médio de onde parte a diagonal, tendo como raio essa diagonal;
6. Prolongar o lado do quadrado até encontrar a circunferência (este novo segmento é o comprimento do retângulo de ouro)

Relativamente a esta divisão, o matemático alemão Zeizing formulou, em 1855, o seguinte princípio:

“Para que um todo dividido em duas partes desiguais pareça belo do ponto de vista da forma, deve apresentar a parte menor e a maior a mesma relação que entre esta e o todo.”

A divisão de um segmento feita segundo essa proporção denomina-se divisão áurea, a que Euclides chamou divisão em média e extrema razão, também conhecida por secção divina pelo matemático Luca Pacioli ou secção áurea segundo Leonardo da Vinci.

O número de ouro é representado pela letra , em homenagem a Fídias (Phideas), famoso escultor grego, por ter usado a proporção de ouro em muitos dos seus trabalhos.

Espiral de ouro

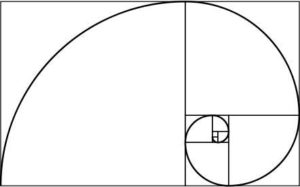
Um retângulo de ouro tem a interessante propriedade: se o dividirmos num quadrado e num retângulo, o novo retângulo é também de ouro. Repetido este processo infinitamente e unidos os cantos dos quadrados gerados, obtém-se uma espiral a que se dá o nome de espiral de ouro.

Fontes:

• Enciclopédia do Estudante;
• LISA – A BIBLIOTECA DA MATEMÁTICA MODERNA.

Veja também:

• Razões e Proporções