Leia o artigo: Circunferência
01. (USP) Os lugar geométrico dos pontos de coordenadas (x; y) tais que y2 + (x – 1)2 = 0 é:
a) a origem
b) duas retas concorrentes
c) um ponto que não é a origem
d) conjunto vazio
e) uma reta.
02. (USP) A equação da reta perpendicular ao eixo das abscissas que passa pelo ponto médio do segmento AB, onde A(2, 3) e B é o centro da circunferência de equação x2 + y2 – 8x – 6y + 24 = 0, é:
a) y = 3
b) y = 4
c) x = 4
d) x = 3
e) 3x + 4y = 0
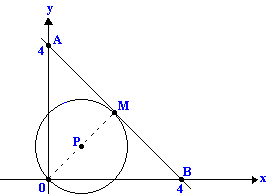
03. (USP) Se M é o ponto médio do segmento AB e P é o ponto médio do segmento OM, determinar a equação da circunferência de centro P e raio OP.
04. Determinar a equação da tangente à circunferência x2 + y2 – 2x – 4y + 1 = 0 pelo ponto P(-1; 2).
05. Determinar as equações das retas (t) tangentes à circunferência x2 + y2 + 2x – 3 = 0 e que passam pelo ponto P(5, 2).
06. (UEMT) Dada a circunferência C da equação (x – 1)2 + y2 = 1 e considerando o ponto P(2, 1), então as retas tangentes a C passando por P:
a) Têm equações y = 1 e x = 2.
b) não existem pois P é interno a C.
c) são ambas paralelas à reta y =1
d) Têm equações y = 1 (e só uma porque P está em C).
c) Têm equações x = 1 e y = 2.
07. A equação da circunferência que passa pelo ponto (2,0) e que tem centro no ponto (2, 3) é dada por:
a) x2 + y2 – 4x – 6y + 4 = 0
b) x2 + y2 – 4x – 9y – 4 = 0
c) x2 + y2 – 2x – 3y + 4 = 0
d) 3x2 + 2y2 – 2x – 3y – 4 = 0
e) (x – 2)2 + y2 = 9
08. A equação da circunferência que passa pelo ponto A = (0; 2) e é tangente na origem a reta r y + 2x = 0, é:
a) x2 + y2 – 2x – y = 0
b) x2 + y2 + 4x – 2y = 0
c) x2 + y2 – 4x – 2y = 0
d) x2 + y2 + 4x + 2y = 0
e) x2 + y2 + 4x + 2y = 0
09. A equação da circunferência que tangencia as retas x + y = 0 e x + y = 8 e que passa pelo ponto (0; 0) é:
a) 2 . x2 + 2y2 – 4x – 4y = 0
b) x2 + y2 – 2x – 6y = 0
c) x2 + y2 – 4x – 4y = 0
d) x2 + y2 + 4x + 4y = 0
e) n.d.a.
10. A equação da reta tangente à circunferência (x – 4)2 + (y – 5)2 = 20 e que a tangencia no ponto de abscissa 2 é:
a) x – 2y – 4 = 0
b) x + 2y – 4 = 0 e x – 2y + 16 = 0
c) x + y – 2 = 0 e x – y + 16 = 0
d) x + 2y – 4 = 0 e x – 2y + 4 = 0
e) n.d.a.
Respostas:
01. C
02. D
03. (x – 1)2 + (y-1)2 = 2
04. x + 1 = 0
05. y – 2 = 0 e 3x – 4y – 7 = 0
| 06. A | 07. A | 08. C | 09. C |
| 10. B |