1. O grau de uma função
O grau de uma variável independente é dado pelo seu expoente. Assim, as funções de segundo grau são dadas por um polinômio de segundo grau, e o grau do polinômio é dado pelo monômio de maior grau.
Portanto, as funções de segundo grau têm a variável independente com grau 2, ou seja, o seu maior expoente é 2. O gráfico que corresponde a essas funções é uma curva denominada parábola.
No dia-a-dia, há muitas situações definidas pelas funções de segundo grau. A trajetória de uma bola lançada para a frente é uma parábola. Se fizermos vários furos em várias alturas num bote cheio de água, os pequenos jorros de água que saem pelos furos descrevem parábolas. A antena parabólica tem a forma de parábola, originando o seu nome.
2. Definição
Em geral, uma função quadrática ou polinomial do segundo grau é expressa da seguinte forma:
align=”center”>
f (x) = ax2 + bx + c, onde a |
Observamos que aparece um termo de segundo grau, ax2. É essencial que exista um termo de segundo grau na função para que ela seja uma função quadrática, ou de segundo grau. Além disso, esse termo deve ser o de maior grau da função, pois se houvesse um termo de grau 3, isto é, ax3, ou de grau superior, estaríamos falando de uma função polinomial de terceiro grau.
Assim como os polinômios podem ser completos ou incompletos, temos funções de segundo grau incompletas, como:
align=”center”>
f (x) = x2 |
Pode acontecer de o termo de segundo grau aparecer isoladamente, como na expressão geral y = ax2; acompanhado por um termo de primeiro grau, como no caso geral y = ax2 + bx; ou também unido a um termo independente ou a um valor constante, como em y = ax2 + c.
É comum pensarmos que a expressão algébrica de uma função quadrática é mais complexa que a das funções lineares. Normalmente, também supomos que sua representação gráfica é mais complicada. Mas não é sempre assim. Além disso, os gráficos das funções quadráticas são curvas muito interessantes, conhecidas como parábolas.
3. Representação gráfica da função y = ax2
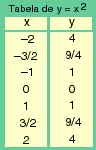
Como acontece com toda função, para representá-la graficamente temos, antes, de construir uma tabela de valores (Figura 3, ao lado).
Começamos representando a função quadrática y = x2, que é a expressão mais simples da função polinomial de segundo grau.
Se unirmos os pontos com uma linha contínua, o resultado é uma parábola, como mostra a Figura 4, abaixo:
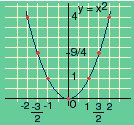
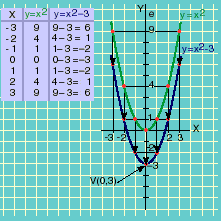
Observando atentamente a tabela de valores e a representação gráfica da função y = x2 vamos perceber que o eixo Y, das ordenadas, é o eixo de simetria do gráfico.
align=”center”>
Além disso, o ponto mais baixo da curva (aquele em que a curva se intercepta com o eixo Y) é o ponto de coordenadas (0, 0). Este ponto é conhecido como vértice da parábola. |
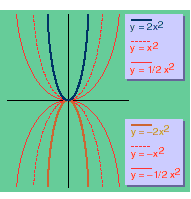
Na Figura 5, ao lado, estão as representações gráficas de várias funções que têm como expressão geral y = ax2.
Observando com atenção a Figura 5 podemos afirmar:
• O eixo de simetria de todos os gráficos é o eixo Y.
Como x2 = (– x)2, a curva é simétrica em relação ao eixo das ordenadas.
• A função y = x2 é crescente para x > xv e decrescente para x < xv. Trata-se de uma função contínua, pois para pequenas variações de x correspondem pequenas variações de y.
• Todas as curvas têm o vértice no ponto (0,0).
• Todas as curvas que estão no semiplano de ordenadas positivas, com exceção do vértice V (0,0), têm ponto de mínimo que é o próprio vértice.
• Todas as curvas que estão no semiplano de ordenadas negativas, com exceção do vértice V (0,0), têm ponto de máximo que é o próprio vértice.
• Se o valor de a for positivo, os ramos da parábola se dirigem para cima. Ao contrário, se a for negativo, os ramos se dirigem para baixo. Dessa forma, o sinal do coeficiente determina a orientação da parábola:
align=”center”>
a > 0, a parábola abre-se para valores positivos de y. a < 0, a parábola abre-se para valores negativos de y. |
• | À medida que aumenta o valor absoluto de a, a parábola é mais fechada, isto é, os ramos ficam mais próximos do eixo de simetria: quanto maior |a|, mais a parábola se fecha. |
• | Os gráficos de y = ax2 e y = –ax2 são simétricos entre si com relação ao eixo X, das abscissas. |
align=”center”>
align=”center”>