Um Sistema de Equações Lineares é um conjunto ou uma coleção de equações com as quais é possível lidar de uma única vez. Sistemas Lineares são úteis para todos os campos da matemática aplicada, em particular, quando se trata de modelar e resolver numericamente problemas de diversas áreas. Nas engenharias, na física, na biologia, na química e na economia, por exemplo, é muito comum a modelagem de situações por meio de sistemas lineares.
De maneira geral, um Sistema de Equações Lineares pode ser definido como um conjunto de m equações, sendo m ≥ 1, com n incógnitas x1, x2, x3, … xn, de forma que:
a11x1 + a12x2 + … + a1nxn = b1
a21x1 + a22x2 + … + a2nxn = b2
…
am1x1 + am2x2 + … + amnxn = bm
Sendo que: a1, …, an e b são números reais. Os números aij são os coeficientes angulares e bi é o termo independente e quando este é nulo a equação linear é chamada homogênea.
Exemplo:
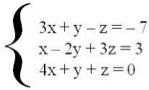
O sistema linear acima possui três equações, três incógnitas (x, y, z) e os termos independentes, que são – 7, 3 e 0. Além disso, no sistema acima há uma equação homogênea (4x + y + z = 0).
Um sistema linear também pode ser escrito em forma matricial. A seguir, a função apresentada no exemplo anterior será exposta em forma de matriz:
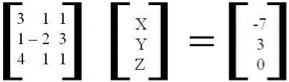
Percebe-se que a forma matricial de um sistema linear é igual ao produto matricial entre a matriz formada pelos coeficientes angulares e a matriz formada pelas incógnitas, cujo resultado é a matriz formada pelos termos independentes.
Solução de um Sistema Linear
A solução de um sistema linear é um conjunto de valores que satisfaz ao mesmo tempo todas as equações de um sistema linear, ou seja, a ênupla ordenada (sequência ordenada de n elementos) é solução de um sistema linear S, se for solução de todas as equações de S.
Exemplo:
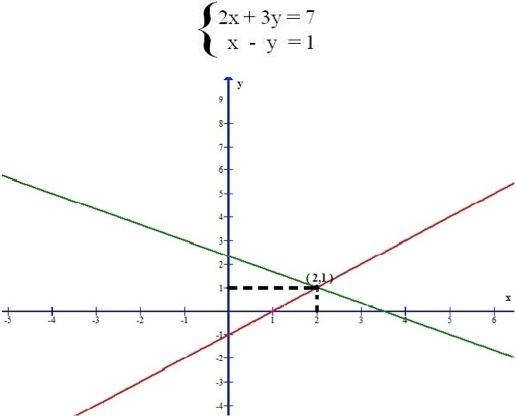
Os valores que satisfazem as duas equações são x = 2 e y = 1, logo, a solução do sistema é o par ordenado (2,1), como mostra a representação gráfica do sistema linear apresentado como exemplo.
Quando um ocorre um Sistema Linear Homogênio, aquele que possui todas as equações com termos independentes nulos, ele admite uma solução nula (0, 0, …, 0) chamada de solução trivial. Mas, um sistema linear homogênio pode ter outras soluções além da trivial.
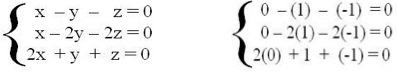
O sistema linear acima é homogêneo, portanto, a priori, já temos a solução trivial dada pelo conjunto (0, 0, 0). Contudo, também se admite como solução desse sistema o conjunto (0, 1, – 1).
A partir de agora, serão apresentados dois métodos para a obtenção do conjunto verdade de um sistema: a Regra de Cramer e o Escalonamento.
Regra de Cramer
É aplicável na resolução de um sistema n x n incógnitas, no qual o determinante diferente de zero (D ≠ 0). Ou seja: (x1 = D1 / D, x2 = D2 / D, …, xn = Dn / D). Sendo que, ao considerar o sistema:
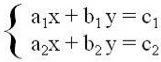
Percebe-se que os coeficientes a1 e a2se relacionam com a incógnita x, enquanto b1 e b2 e se relacionam com a incógnita y. Agora, a partir da matriz incompleta:
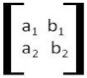
É possível obter o determinante (D) desta matriz e substituindo os coeficientes de x e y que o compõe pelos termos independentes c1e c2 é possível encontrar os determinantes Dx e Dy para que se aplique a Regra de Cramer. Abaixo estão os referidos determinantes:
![]() Exemplo:
Exemplo:
Então: x = Dx/D = -10/-5 = 2 e y = Dy/D = -5/-5 = 1, portanto, como foi mostrado anteriormente, inclusive graficamente, o par ordenado (2,1) é o resultado do sistema linear acima.
Escalonamento
Um sistema está escalonado quando de equação para equação, no sentido de cima para baixo, houver aumento dos coeficientes nulos situados antes dos coeficientes não nulos. Exemplo:

O sistema acima está escalonado e substituindo as incógnitas das equações pelos seus respectivos é possível encontrarmos o conjunto solução (1,1,1).
Para escalonar um sistema é necessário que se coloque como primeira equação aquela que tenha o coeficiente de valor 1 na primeira incógnita. Caso não haja nenhuma equação assim, será necessário dividir membro a membro aquela que está como primeira equação pelo coeficiente da primeira incógnita. Nas demais equações, é necessário que se obtenha zero como coeficiente da primeira incógnita, somando cada uma delas com o produto da primeira equação pelo oposto do coeficiente dessa incógnita, até que se possam verificar os valores de cada uma das incógnitas e, por fim, encontrar o conjunto solução.
Referências Bibliográficas
COXFORD, Arthur F., PAYNE, Joseph N. Advanced Mathematics: A Preparation for Calculus – Harcourt Brace Javanovich Inc. – 1972
http://www.ime.usp.br/~colli/cursos/NumericoIAG-2005/LivroNumericoCapitulos1-2-3.pdf
http://www-math.sp2mi.univ-poitiers.fr/~arnaud/L1SPIC11/correction_systemes.pdf
Por: Anderson Andrade Fernandes