As equações são classificadas de acordo com o número de incógnitas e o grau destas. As equações de primeiro grau são denominadas assim porque o grau da incógnita (termo x) é 1 (x = x1).
Equação de 1º grau com uma incógnita
Denominamos equação do 1º grau em ℜ, na incógnita x, toda equação que pode ser escrita na forma ax + b = 0, com a ≠ 0, a ∈ ℜ e b ∈ ℜ. Os números a e b são os coeficientes da equação e b é seu termo independente.
A raiz (ou solução) de uma equação com uma incógnita é o número do conjunto universo que, quando substituído pela incógnita, transforma a equação numa sentença verdadeira.
Exemplos
- O número 4 é raiz da equação 2x + 3 = 11, pois 2 · 4 + 3 = 11.
- O número 0 é raiz da equação x2 + 5x = 0, pois 02 + 5 · 0 = 0.
- O número 2 não é raiz da equação x2 + 5x = 0, pois 22 + 5 · 2 = 14 ≠ 0.
Equação de 1º grau com duas incógnitas
Denominamos equação do 1º grau em ℜ, nas incógnitas x e y, toda equação que pode ser escrita na forma ax + by = c, em que a, b e c são números reais com a ≠ 0 e b ≠ 0.
Considerando a equação com duas incógnitas 2x + y = 3, observamos que:
- para x = 0 e y = 3, temos 2 · 0 + 3 = 3, que é uma sentença verdadeira. Dizemos, então, que x = 0 e y = 3 é uma solução da equação dada.
- para x = 1 e y = 1, temos 2 · 1 + 1 = 3, que é uma sentença verdadeira. Então, x = 1 e y = 1 é uma solução da equação dada.
- para x = 2 e y = 3, temos 2 · 2 + 3 = 3, que é uma sentença falsa. Então, x = 2 e y = 3 não é solução da equação dada.
Resolução passo a passo de equações de 1º grau
Resolver uma equação significa encontrar o valor da incógnita que verifica a igualdade algébrica.
Exemplo 1
Resolver a equação 4(x – 2) = 6 + 2x:
1. Eliminar os parênteses.
Para eliminar os parênteses, multiplicar cada um dos termos de dentro dos parênteses pelo número de fora (inclusive seu sinal):
4(x – 2) = 6 + 2x
4x – 8 = 6 + 2x
2. Efetuar a transposição de termos.
Para resolver equações é possível eliminar termos somando, subtraindo, multiplicando ou dividindo (por números diferentes de zero) nos dois membros.
Para abreviar esse processo, pode-se fazer com que um termo que aparece em um membro apareça de forma inversa no outro, ou seja:
- se está somando em um membro, aparece subtraindo no outro; se está subtraindo, aparece somando.
- se está multiplicando em um membro, aparece dividindo no outro; se está dividindo, aparece multiplicando.
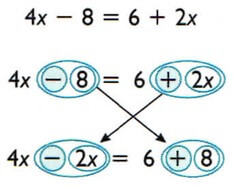
3. Reduzir os termos semelhantes:
4x – 2x = 6 + 8
2x = 14
4. Isolar a incógnita e encontrar seu valor numérico:
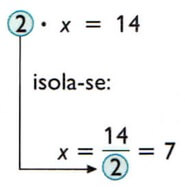
Solução: x = 7
Obs: os passos 2 e 3 podem se repetir.
[latexpage]
Exemplo 2
Resolver a equação: 4(x – 3) + 40 = 64 – 3(x – 2).
- Eliminar os parênteses: 4x -12 + 40 = 64 – 3x + 6
- Reduzir os termos semelhantes: 4x + 28 = 70 – 3x
- Efetuar a transposição de termos: 4x + 28 + 3x = 70
- Reduzir os termos semelhantes: 7x + 28 = 70
- Efetuar a transposição de termos: 7x = 70 – 28
- Reduzir os termos semelhantes: 7x = 42
- Isolar a incógnita e encontrar a solução: $\mathrm{x= \frac{42}{7} \rightarrow x = \textbf{6}}$
- Comprovar que a solução obtida está correta:
4(6 – 3) + 40 = 64 – 3(6 – 2)
12 + 40 = 64 – 12 → 52 = 52
Exemplo 3
Resolver a equação: 2(x – 4) – (6 + x) = 3x – 4.
- Eliminar os parênteses: 2x – 8 – 6 – x = 3x – 4
- Reduzir os termos semelhantes: x – 14 = 3x – 4
- Efetuar a transposição de termos: x – 3x = 14 – 4
- Reduzir os termos semelhantes: – 2x = 10
- Isolar a incógnita e encontrar a solução: $\mathrm{x= \frac{- 10}{2} \rightarrow x = \textbf{- 5}}$
- Comprovar que a solução obtida está correta:
2(-5 – 4) – (6 – 5) = 3(-5) – 4 =
2 (-9) – 1 = -15 – 4 → -19 = -19
Como resolver problemas com equações de 1º grau
Vários problemas podem ser resolvidos aplicando uma equação do primeiro grau. Em geral, devem ser seguidos estes passos ou fases:
- Compreensão do problema. O enunciado do problema deve ser lido detalhadamente para identificar os dados e o que se deve obter, a incógnita x.
- Montagem da equação. Consiste em traduzir o enunciado do problema em linguagem matemática, por meio de expressões algébricas, para obter uma equação.
- Resolução da equação obtida.
- Comprovação e análise da solução. É necessário comprovar se a solução obtida é correta e, depois, analisar se tal solução tem sentido no contexto do problema.
Exemplo 1:
- Ana tem 2,00 reais a mais que Berta, Berta tem 2,00 reais a mais que Eva e Eva, 2,00 reais a mais que Luisa. As quatro amigas juntas possuem 48,00 reais. Quantos reais cada uma delas tem?
1. Compreender o enunciado: Deve-se ler o problema quantas vezes forem necessárias para distinguir os dados conhecidos e os dados desconhecidos que se deseja encontrar, isto é, a incógnita.
2. Montar a equação: Escolher como incógnita x a quantidade de reais que Luísa tem.
Quantidade de reais que Luísa tem: x.
Quantidade que Eva tem: x + 2.
Quantidade que Berta tem: (x + 2) + 2 = x + 4.
Quantidade que Ana tem: (x + 4) + 2 = x + 6.
3. Resolver a equação: Escrever a condição de que a soma é 48:
x + (x + 2) + (x + 4) + (x + 6) = 48
4 • x + 12 = 48
4 • x = 48 – 12
4 • x = 36
x = 9.
Luísa tem 9,00, Eva, 11,00, Berta, 13,00, e Ana, 15,00.
4. Comprovar:
As quantidades que possuem são: 9,00, 11,00, 13,00 e 15,00 reais. Eva tem 2,00 reais a mais que Luísa, Berta, 2,00 a mais que Eva e assim por diante.
A soma das quantidades é 48,00 reais: 9 + 11 + 13 + 15 = 48.
Exemplo 2:
- A soma de três números consecutivos é 48. Quais são eles?
1. Compreender o enunciado. Trata-se de encontrar três números consecutivos.
Se o primeiro for x, os outros serão (x + 1) e (x + 2).
2. Montar a equação. A soma desses três números é 48.
x + (x + 1) + (x + 2) = 48
3. Resolver a equação.
x + x + 1 + x + 2 = 48
3x + 3 = 48
3x = 48 – 3 = 45
$\mathrm{x= \frac{45}{3} = \textbf{15}}$
Os números consecutivos são: 15, 16 e 17.
4. Comprovar a solução.
15 + 16 + 17 = 48 → A solução é válida.
Exemplo 3:
- Uma mãe tem 40 anos e seu filho, 10. Quantos anos transcorrerão para que a idade da mãe seja o triplo da idade do filho?
1. Compreender o enunciado.
| Hoje | Dentro de x anos | |
|---|---|---|
| Idade da mãe | 40 | 40 + x |
| Idade do filho | 10 | 10 + x |
2. Montar a equação.
40 + x = 3(10 + x)
3. Resolver a equação.
40 + x = 3(10 + x)
40 + x = 30 + 3x
40 – 30 = 3x – x
10 = 2x
$\mathrm{x= \frac{10}{2} = \textbf{5}}$
4. Comprovar a solução.
Dentro de 5 anos: a mãe terá 45 anos e o filho, 15.
Verifica-se: 45 = 3 • 15
Exemplo 4:
- Calcular as dimensões de um retângulo sabendo que sua base é quatro vezes sua altura e seu perímetro mede 120 metros.
Perímetro = 2 (a + b) = 120
Do enunciado: b = 4a
Portanto:
2(a + 4a) = 120
2a + 8a = 120
10a = 120
$\mathrm{a= \frac{120}{10} = \textbf{12}}$
Se a altura é a = 12, a base é b = 4a = 4 • 12 = 48
Comprovar que 2 • (12 + 48) = 2 • 60 = 120
Exemplo 5:
- Em uma fazenda há coelhos e galinhas. Se as cabeças forem contadas, haverá 30 e, no caso das patas, haverá 80. Quantos coelhos e quantas galinhas há?
Ao chamar de x o número de coelhos, então 30 – x será o número de galinhas.
Cada coelho tem 4 patas e cada galinha, 2; logo, a equação é: 4x + 2(30 – x) = 80
E sua resolução:
4x + 60 – 2x = 80
4x – 2x = 80 – 60
2x = 20
$\mathrm{x= \frac{20}{2} = \textbf{10}}$
Existem 10 coelhos e 30 – 10 = 20 galinhas.
Comprovar que 4 • 10 + 2 • (30 – 10) = 40 + 40 = 80
Por: Paulo Magno da Costa Torres