O conceito de juros está ligado diretamente ao conceito de capital. Este pode ser denominado como valor de quantia monetária transacionada e também pode ser chamado de principal.
Esses conceitos estão diretamente relacionados com comportamentos de consumo e disponibilidade de renda em função do tempo, conforme a renda que as pessoas recebem no presente e conforme as preferências intertemporais de consumo dessas pessoas.
Um padrão de consumo pode ser maior do que suas rendas no presente, em troca de um consumo menor no futuro, ou pode ser menor e com disposição a poupança de renda para consumo futuro.
Assim, de um lado há a demanda por crédito e do outro a oferta de fundos, que supre a necessidade essa demanda por crédito. Chama-se taxa de juros ao valor do juro em uma unidade de tempo, expresso como porcentagem do capital.
Juros Simples
Considerando um capital C, aplicado a juros simples e à taxa t, durante n períodos de tempo, é possível deduzir a seguinte regra (fórmula) de juros após n períodos de aplicação:
 Juros após um período: J1 = C.t
Juros após um período: J1 = C.t- Juros após dois períodos: J1 = C.t + C.t = 2.(C.t)
- Juros após três períodos: J1 = C.t + C.t + C.t = 3.(C.t)
- Juros após n períodos: Jn = C.t + C.t + … + C.t = n.(C.t)
Portanto, lembrando que C é o capital, t é a taxa de juros e n é o período de aplicação, a fórmula para calcular juros simples é:
Antes da exposição de exemplos, é importante que se fale sobre o conceito de montante.
Montante
Chama-se montante de um investimento (ou de um empréstimo) à soma do capital com o juro obtido pela aplicação (ou pago pelo empréstimo). Sendo C o capital, J o juro, t a taxa de juro e M o montante e baseando-se na definição acima se obtém:
Com base nas relações expostas acima, para cálculo de juros simples e cálculo do montante de um investimento, é possível verificar que a equação para a obtenção da taxa de jurost, quando dados os valores C e M, é:
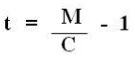
Pode-se comprovar a relação acima por meio da seguinte demonstração:
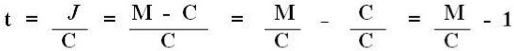
Exemplos de como calcular:
1 – Um capital de R$ 1.000,00 é aplicado durante um mês, à uma taxa de 1,1% ao mês.
(a) Qual é o juro no período?
(b) Qual é o valor do montante?
Repostas:
(a) J = 1000 . 1,1% = 1000 . 0,011 = 11; portanto, o juro é igual a R$ 11,00.
(b) M = 1000 + 11 = 1011; portanto, o montante é igual a R$ 1.011,00.
2 – Um capital de R$ 700.000,00 é aplicado durante um ano, à uma taxa de 30% ao ano.
(a) Qual é o juro no período?
(b) Qual é o valor do montante?
Respostas:
(a) J = 700000 . 30% = 700000 . 0,3 = 210000; portanto, o juro é igual a R$ 210.000,00.
(b) M = 700000 + 210000 = 910000; portanto o montante é igual a R$ 910.000,00.
3 – Um capital de R$ 12.000,00 foi aplicado durante três meses, produzindo um montante de R$ 14.640,00. Qual é a taxa trimestral de juros?
Resposta:
t = (M / C) – 1 = (14640 / 12000) – 1 = 1,22 – 1 = 0,22; portanto, a taxa de juros é de 22% ao trimestre.
4 – Qual o capital que rende juros de R$ 3.000,00 durante cinco meses, se a taxa de juros simples for 2% ao mês?
Reposta:
Sendo t = 2% a.m., o número de meses n = 5e o juros J = 3000, obtém-se:3000 = C . 2% . 5
3000 = C . 0,02 . 5
3000 = C . 0,1
C = 3000 / 0,1 = 30000
Portanto, o capital possui o valor de R$ 30.000,00.
Por fim, com base no que foi exposto anteriormente, é possível verificar que somente o capital inicial rende juros, portanto só se calcula juros simples sobre o capital inicial C. Além disso, é importante verificar que o ganho obtido se dá como uma sequência linear.
Juros Compostos
Pode-se dizer que os juros compostos são, simplesmente, juros sobre juros. Sendo assim, pode-se concluir que os juros não incidiram somente sobre o capital inicial, mas também sobre os juros que foram anteriormente capitalizados, por isso o ganho obtido se dá como uma sequência geométrica.
Considerando um capita C, uma taxa de juros t e calculando o montante obtido a juros compostos, após n período de tempo, obtém-se:
Inicialmente, o capital inicial C;
- Montante após um período: M1 = C + C.t = C(1 + t)1
- Montante após dois períodos: M2 = M1 + M1 . t = M1(1 + t) = C(1 + t)2
- Montante após três períodos: M3 = M2 + M2 . t = M2(1 + t) = C(1 + t)3
Generalizando, é obtida a seguinte fórmula:
Mn = C (1 + t)n
Exemplo de como calcular:
Calcule os juros produzidos por uma aplicação de R$ 8.000,00 em 4 meses a uma taxa de 6% a.m. com juros compostos.
Reposta:
Primeiramente, encontrar o montante. Considerando C = 8000, t = 6 / 100 = 0,06 e n = 4, obtém-se:
M4 = 8000 (1 + 0,06)4
M4 = 10099,81
O cálculo dos juros produzidos é possível se do montante encontrado for subtraído o valor do capital C, logo: J = M4 – C.
J = 10099,81 – 8000 = 2099, 81
Portanto, os juros produzidos foram de R$ 2.099,81.
Referência Bibliográfica
Hazzan, Samuel e Pompeo, José Nicolau. Matemática Financeira. São Paulo, Atual, 1987
https://www.ime.usp.br/arquivos/4congresso/39%20Estela%20Mara%20de%20Oliveira_N.pdf
Por: Anderson Andrade Fernandes
 Juros após um período: J1 = C.t
Juros após um período: J1 = C.t