Função Exponencial

Uma função é uma maneira de associar a cada valor do argumento x um único valor da função f(x). Isto pode ser feito especificando através de uma fórmula um  relacionamento gráfico entre diagramas representando os dois conjuntos, e/ou uma regra de associação, mesmo uma tabela de correspondência pode ser construída.

Entre conjuntos numéricos é comum representarmos funções por seus gráficos, cada par de elementos relacionados pela função determina um ponto nesta representação, a restrição de unicidade da imagem implica em um único ponto da função em cada linha de chamada do valor independente x.

As funções exponenciais são aquelas que crescem ou decrescem muito rapidamente. Elas desempenham papéis fundamentais na Matemática e nas ciências envolvidas com ela, como: Física, Química, Engenharia, Astronomia, Economia, Biologia, Psicologia e outras.

A função exponencial é a definida como sendo a inversa da função logarítmica natural, isto é:

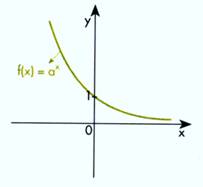
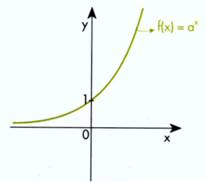
GRÁFICOS DA FUNÇÃO EXPONENCIAL

PROPRIEDADES DA FUNÇÃO EXPONENCIAL

Se a, x e y são dois números reais quaisquer e k é um número racional, então:

• a^x a^y= a^{x + y}
• a^x / a^y= a^{x – y}
• (a^x) ^y= a^x.y
• (a b)^x = a^x b^x
• (a / b)^x = a^x / b^x
• a^-x = 1 / a^x

Estas relações também são válidas para exponenciais de base e (e = número de Euller = 2,718…)

• y = e^x se, e somente se, x = ln(y)
• ln(e^x) =x
• e^x+y= e^x.e^y
• e^x-y = e^x/e^y
• e^x.k = (e^x)^k

A CONSTANTE DE EULER

Existe uma importantíssima constante matemática definida por

e = exp(1)

O número e é um número irracional e positivo e em função da definição da função exponencial, temos que:

Ln(e) = 1

Este número é denotado por e em homenagem ao matemático suíço Leonhard Euler (1707-1783), um dos primeiros a estudar as propriedades desse número.

O valor deste número expresso com 40 dígitos decimais, é:

e = 2,718281828459045235360287471352662497757

Se x é um número real, a função exponencial exp(.) pode ser escrita como a potência de base e com expoente x, isto é: