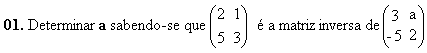


04. Sendo A e B matrizes inversíveis de mesma ordem, resolver a equação matricial A.X.At = B.
05. Seja Q uma matriz 4 x 4 tal que det Q = 0 e Q3 + 2Q2 = 0. Calcule det Q.
06. Demonstrar que (AB)-1 = B-1 . A-1, desde que as matrizes A e B sejam inversíveis e de mesma ordem.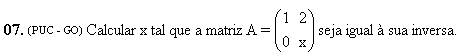
08. (PUC) Sendo A e B matrizes inversíveis de mesma ordem e X uma matriz tal que (X . A)t = B, então:
a) X = A-1 . Bt
b) X = Bt . A-1
c) X = (B . A)t
d) X = (AB)t
e) X = At . B-1
09. No que se refere à solução da equação A . X = B em que A e B são matrizes quadradas de ordem 3, pode-se dizer que:
a) a equação não pode ter solução;
b) a equação nunca tem solução;
c) a equação tem sempre uma solução que é X = B ;
A
d) a equação tem sempre uma solução que é X = B . A-1
e) a equação tem sempre uma solução que é X = A-1 . B.
10. (ITA) Sejam A e B matrizes reais quadradas de ordem 2 que satisfazem a seguinte propriedade: existe uma matriz M inversível tal que A = M-1 BM. Então:
a) det (-At) = det B
b) det A = -det B
c) det (2A) = 2 det B
d) Se det B ¹ 0, então det (-AB) < 0
e) det (A – I) = -det (I – B)
Leia os artigos: Matrizes e Operações com Matrizes
Respostas:
01. a = -1
02. a = 2
03. a = 15
04. V = {A-1 . B . (At)-1}
05. det Q = 16
06. Lembrando que AB = I Þ A-1 = B e que a multiplicação de matrizes é associativa, temos:
(AB) . (B-1 . A-1) = A . (B . B-1) . A-1 = A . I . A-1 = A . A-1 = I
Se (AB) . (B-1 . A-1) = I, então (AB)-1 = B-1 . A-1
07. R = -1
08. B
09. A
10. A