Chamamos Progressão Geométrica (P.G.) a uma sequência de números reais, formada por termos, que a partir do 2º, é igual ao produto do anterior por uma constante q dada, chamada de razão da P.G.
Dada uma sequência (a1, a2, a3, a4, …, an,…), então se ela for uma P.G. ![]() an = an-1 . q, com n
an = an-1 . q, com n![]() 2 e n
2 e n![]() IN, onde:
IN, onde:
a1 – 1º termo
a2 = a1. q ![]()
![]()
a3 = a2. q² ![]()
![]()
a4 = a3. q³ ![]()
![]() .
.
an = an-1. q ![]()
![]()
CLASSIFICAÇÃO DAS PROGRESSÕES GEOMÉTRICAS P.G.s
1. Crescente:
2. Decrescente:
3. Alternante ou Oscilante: quando q < 0.
4. Constante: quando q = 1
5. Estacionária ou Singular: quando q = 0
FÓRMULA DO TERMO GERAL DE UMA PROGRESSÃO GEOMÉTRICA
Vamos considerar uma P.G. (a1, a2, a3, a4,…, an,…). Pela definição temos:
a1 = a1
a2 = a1. q ![]()
![]()
a3 = a2. q² ![]()
![]()
a4 = a3. q³ ![]()
![]() .
.
an = an-1. q ![]()
![]()
Depois de multiplicarmos os dois membros das igualdades e simplificarmos, vem:
an = a1.q.q.q….q.q
(n-1 fatores)
an = a1
Termo Geral da P.A.
INTERPOLAÇÃO GEOMÉTRICA
Interpolar, Inserir ou Intercalar m meios geométricos entre dois números reais a e b significa obter uma P.G. de extremos a e b, com m+2 elementos. Podemos resumir que problemas envolvendo interpolação se reduzem em calcularmos a razão da P.G. Mais à frente resolveremos alguns problemas envolvendo Interpolação.
SOMA DOS TERMOS DE UMA P.G. FINITA
Dada a P.G. (a1, a2, a3, a4, …, an-1, an…), de razão ![]() e a soma Sn de seus n termos pode ser expressa por:
e a soma Sn de seus n termos pode ser expressa por:
Sn = a1+a2+a3+a4… +an(Eq.1) Multiplicando ambos os membros por q, vem:
q.Sn = (a1+a2+a3+a4… +an).q
q.Sn = a1.q+a2.q+a3 +.. +an.q (Eq.2) . Encontrando a diferença entre a (Eq.2) e a (Eq.1),
temos:
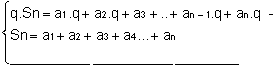
q.Sn – Sn = an . q – a1
![]() Sn(q – 1) = an . q – a1
Sn(q – 1) = an . q – a1![]()
![]() ou
ou
![]() , com
, com ![]()
Obs.: Se a P.G. for constante, isto é, q = 1 a soma Sn será:
![]()
SOMA DOS TERMOS DE UMA P.G. INFINITA
Dada a P.G. infinita: (a1, a2, a3, a4, …), de razão q e S sua soma, devemos analisar 3 casos para calcularmos a soma S.
an = a1.
1. Se a1= 0 ![]() S = 0, pois
S = 0, pois
2. Se q <–1 ou q > 1, isto é ![]() e a1
e a1![]() 0, S tende a
0, S tende a ![]() ou
ou ![]() . Neste caso é impossível calcular a soma S dos termos da P.G.
. Neste caso é impossível calcular a soma S dos termos da P.G.
3. Se –1< q < 1, isto é, ![]() e a1
e a1![]() 0, S converge para um valor finito. Assim a partir da Fórmula da soma dos n termos de uma P.G., vem:
0, S converge para um valor finito. Assim a partir da Fórmula da soma dos n termos de uma P.G., vem:
Quando n tende a ![]() , qn tende a zero, logo:
, qn tende a zero, logo:
![]()
![]() que é a fórmula da soma dos termos de uma P.G. Infinita.
que é a fórmula da soma dos termos de uma P.G. Infinita.
Obs.: S nada mais é do que o limite da Soma dos termos da P.G., quando n tende para ![]() É representada desta forma:
É representada desta forma:
![]()
PRODUTO DOS TERMOS DE UMA P.G. FINITA
Dada a P.G. finita: (a1, a2, a3, …an-1, an), de razão q e P seu produto, que é dado por:
![]() ou
ou ![]()
Multiplicando membro a membro, vem:
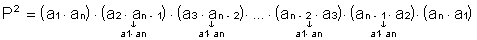
![]() Esta é a fórmula do produto dos termos de uma P.G. finita.
Esta é a fórmula do produto dos termos de uma P.G. finita.
Podemos também escrever esta fórmula de outra forma, pois:
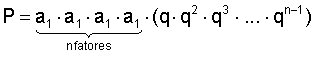
Logo:
